Acho que eu estava no ensino
primário quando ouvi esta história pela primeira vez: um homem precisa
atravessar o rio com uma onça, uma cabra e uma alface. Terá que fazer várias
viagens porque o barco só permite que leve um passageiro de cada vez. Ele não
pode deixar a onça sozinha com a cabra, nem a cabra sozinha com a alface: em
qualquer desses casos, a primeira come a segunda. Como fazer?
Há uma variante ainda mais
interessante deste problema, um jogo que chamarei "humanos e
klingons" (o nome habitual é "missionários e canibais", mas está
baseado em preconceitos culturais que não me agradam).
Três humanos e três klingons
(espécie alienígena muito agressiva) precisam atravessar um rio, usando um
barco no qual cabem no máximo dois passageiros. Se em algum momento os klingons
forem maioria, em qualquer das margens, vão dominar os humanos e matá-los. Como
fazer para transportar os seis para a outra margem, sem risco de massacre?
Brincadeiras como esta podem ser
resolvidas matematicamente usando um conceito muito simples, chamado grafo. Um
grafo é um conjunto de pontos, os vértices, alguns dos quais estão ligados por
curvas, as arestas. Os vértices são usados para representar as diferentes
situações do jogo, e as arestas para descrever as possíveis passagens de uma
situação para a outra.
No caso de "humanos e
klingons", cada situação pode ser descrita indicando o número H de humanos
e o número K de klingons na margem direita, digamos (os demais estão na margem
esquerda, não é necessário especificar).
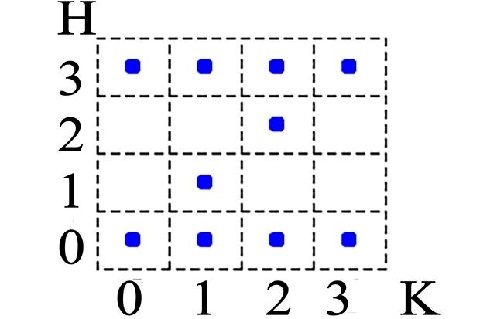
A tabela acima exibe todas as
situações possíveis: são 10 vértices. Os retângulos em branco correspondem aos
casos em que os klingons estariam em maioria, em uma das margens, e teríamos um
massacre de humanos.
Também precisamos acrescentar as
possíveis passagens de uma situação para outra, lembrando que o barco pode
levar e trazer um ou dois passageiros. Isso está feito na tabela abaixo: são 17
arestas.
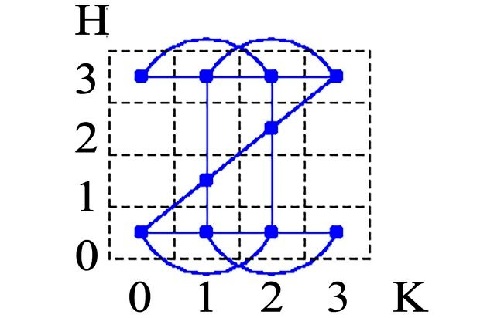 Agora basta procurar neste grafo um
caminho que vá dos pontos H=3 e K=3 (ambos na margem direita) para os pontos
H=0 e K=0 (ambos na margem esquerda) e que esteja formado, alternadamente, por
movimentos para a esquerda ou para baixo e movimentos para a direita ou para
cima. Esta regra corresponde ao fato de que o barco se desloca, alternadamente,
de uma margem para a outra.
Agora basta procurar neste grafo um
caminho que vá dos pontos H=3 e K=3 (ambos na margem direita) para os pontos
H=0 e K=0 (ambos na margem esquerda) e que esteja formado, alternadamente, por
movimentos para a esquerda ou para baixo e movimentos para a direita ou para
cima. Esta regra corresponde ao fato de que o barco se desloca, alternadamente,
de uma margem para a outra.
Pode-se verificar que existem
exatamente quatro soluções para o problema. Uma delas está representada na
figura abaixo: são necessárias 11 viagens do barco, mas todos passam para a
outra margem, sãos e salvos.
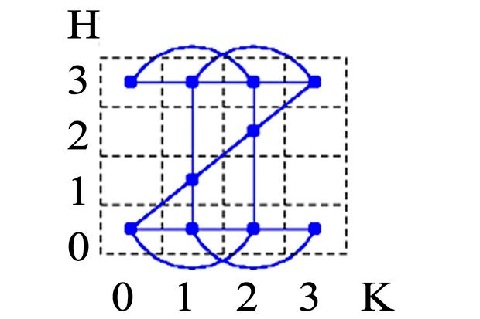
Há muitas variações divertidas das
regras. Numa delas, os passageiros são três casais (humanos): os maridos,
ciumentos, não permitem que suas esposas fiquem sozinhas com outro homem. E o
meu filho (10 anos) me mostrou outra, em que os passageiros são três adultos e
três crianças: as crianças não podem ficar nunca desacompanhadas. Como fazer
para atravessar todo mundo?
Também podemos variar o número de
passageiros. Por exemplo, com quatro humanos e quatro klingons o problema fica
impossível. Mas torna-se novamente possível se o barco puder levar até três
passageiros por vez, com a regra de que os klingons também não podem ser
maioria no barco. Nesse caso fica possível atravessar cinco humanos e cinco
klingons. Mas com seis humanos e seis klingons continua impossível, mesmo com
esse barco maior. Agora, se o barco puder levar quatro passageiros, é possível
fazer atravessar N humanos e N klingons, para qualquer número N.
Será que o leitor é capaz de
utilizar a técnica de grafos para resolver o problema da onça, da cabra e da
alface? Soluções são bem-vindas pelo e-mail: viana.folhasp@gmail.com.
Aproveito para desejar a todos um
ótimo ano de 2018, com muita matemática!
Marcelo Viana - Matemático e diretor-geral do Impa, é ganhador do
Prêmio Louis D., do Institut de France. Aqui, mostra como a matemática pode
transformar vidas e ser divertida.
Fonte: coluna jornal FSP